介绍

协同过滤(Collaborative Filtering,简称CF)是Amazon在2001年提出的应用于推荐领域的一个算法，至今各大家的推荐系统中都能见到协同过滤的影子，是推荐领域最经典的算法之一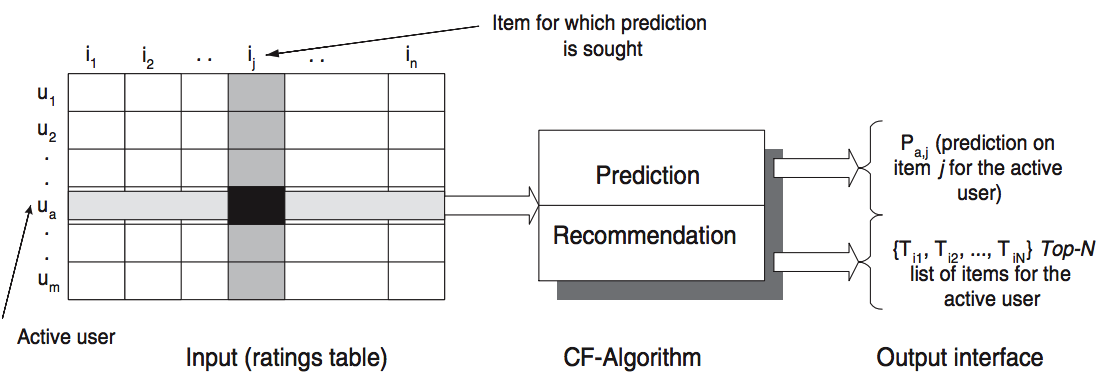

在实际场景中可以将用户对于Item的评分/购买/点击等行为 形成一张user-item的矩阵，单个的User或者Item可以通过对于有交互的Item和User来表示(最简单的就是One-Hot向量)，通过各种相似度算法可以计算到User2User、Item2Item以及User2Item的最近邻，先就假设按User2Item来说:

1. 和你购买相似宝贝的用户,其实和你相近的，也同时认为你们的习惯是相似的，
2. 因此他们买的其他的宝贝你也是可能会去够买的，这批宝贝就可以认为和你相似的

这种场景就非常使用与推荐系统非常匹配了，并且可解释性极强。
但是传统的CF会存在这两个问题:

1. 往往这个矩阵会非常稀疏，大部分稀疏程度在95%以上，甚至会超时99%，这样在计算相似度时就非常不准确了（置信度很低）
2. 整个求最近邻过程中会引入很多Trick，比如平滑、各种阈值等,最终将CF拿到效果还是比较难的。
3. 另外还有一个就是冷启动的问题，新用户或者新的item没法直接使用这种方式来计算

因此后来针对CF提出了不少的优化，主要是对于User/Item的表示从one-Hot的方式想办法转为稠密的方式，假设原生的矩阵我们称之为$R$，如果存在
$$\tilde{R} = UV^T$$

$R=[M,N],U=[M,K],V=[N,K]$,其中$M$为用户量，$N$为Item量

并且使得$\tilde{R} \approx R$,那么我们可以使用$U$来代表用户矩阵，$V$来代表item矩阵，此时每个用户或者item都可以使用一个$K$维来表示，也就是隐向量，他是一个稠密向量，对于one-hot有不少的优势，同时在整个模型中还可以加入其它特征信息，这就是景点的矩阵分解方式(Matrix Factorization，简称MF)，同时对于MF也有不少优化,比如BPR以及最新的MF算法ELAS

一般来说，MF模型得到User和Item的向量之后就可以对这两个向量计算相似度来得到最终的结果，比如我们使用内积的方式:
$$y = f(u,i|U_u,V_i) = U_uV_i^T = \sum_{k=1}^K U_{u,k}V_{i,k}$$
但是其实由于参数空间和隐向量长度$K$限制的问题，对于MF隐向量之间相似度的结果和原生User-Item具体的相似度可能会出现不一致的情况，因此现在的DL盛行的时代，都想在这两个向量上再做一波猛如虎的操作再计算最终的结果，就是本文接下来要说的那些个模型，权当对于CF的最新进展进行一个同步学习:
他们的Task都是可以简化为，给定一个User-Item交互矩阵: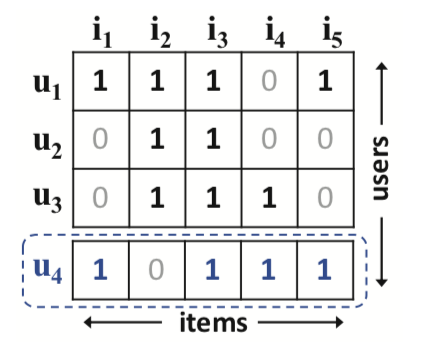

当特定的User和Item输入下计算他们的得分.
$$s = f(u,i|R,\theta) $$

NeuCF

针对MF算法最后通过内积聚合来得到算分的方式，这篇文章的作者认为User和Item的隐向量是相互独立的并且最后是等权重求和，因此他可以使用线性模型来表示，这样支持继续使用神经网络模型来进行加工，所以作者提出了基于神经网络的协同过滤（Neural Collaborative Filtering），说白了就是在隐向量上架MLP层和其他的聚合算子，其中隐向量是通过DL模型自己训练出来的：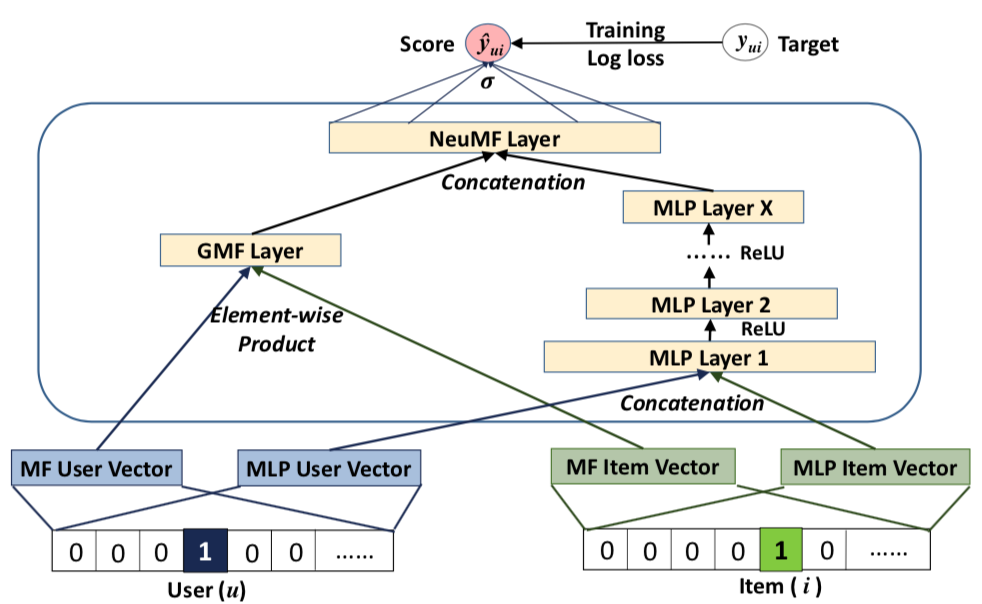

模型主要分两个子模块：GMF（左侧）和 NCF（右侧）:

1. GMF：User和Item的隐向量直接通过element-wise的相乘来进行聚合：$$h_{GMF} = \phi(p_u,q_i) = p_u \odot q_i$$
2. NCF:User和Item的隐向量先进行concat操作，然后过多层的MLP，得到聚合的向量：$$h_{NCF} = \text{mlp}([p_u,q_i],\theta)$$
3. 最后使用concat的方式将两个子模块进行融合$$\hat{y} = \sigma(W^T[h_{GMF},h_{NCF}])$$

由于模型是有两部分组成，因此作者在先使用GMF和NCF分别训练模型，作为pre-train，然后再合并起来将NeuCF模型一起训练，来提升模型的性能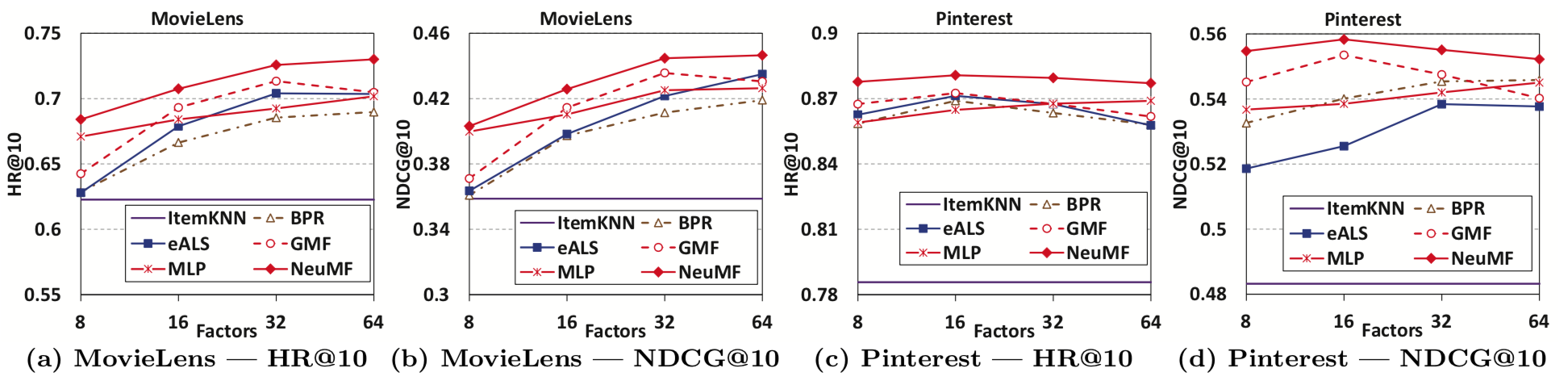

Factor表示模型预测的数量

这里GMF和MLP(NCF)是他的两个子模型，实验结果也可以看到合并起来之后的模型效果要好于子模型，通过也要好于最新的eALS算法。同时作者还，对比了pre-train的效果，确实有不少的提升，具体细节尅看paper。

评一下：整个模型架构简单易懂，使用DL将隐向量做深度的交叉操作，可以继续压榨模型的性能，同时对于该模型用于线上也有很大的可行性。另外关于pre-train部分是否可以使用MF矩阵分解来作为初始化向量会不会更加来的直观一点。

DMF

DMF(Deep Matrix Factorization)的作者受到了DSSM模型的启发:
DSSM中是通过Query对多个Item经过NN网络之间他们的Embedding来计算相似度，作为他们的语义相似，那么这推荐场景下可以迁移为User对于多个Item来计算行为相似度?
因此可以看图: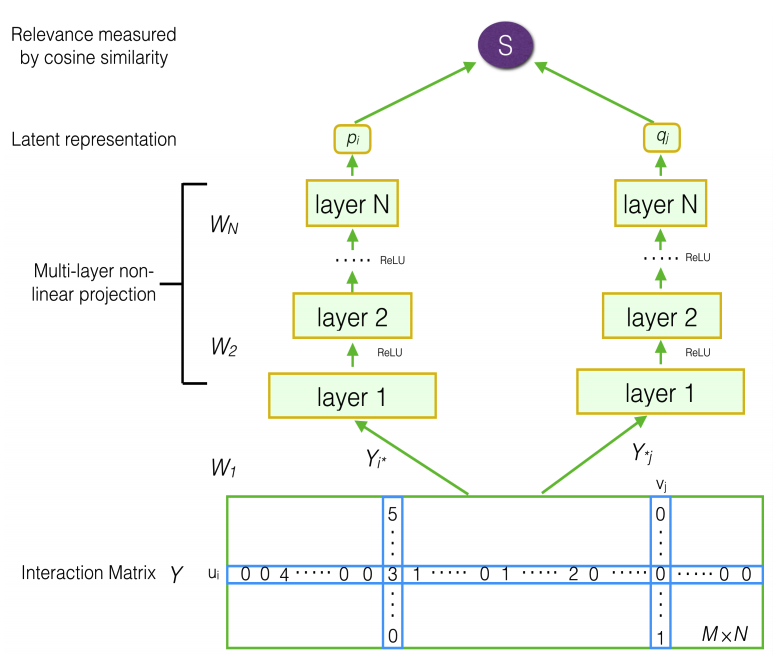

其实这个模型已经很清楚了:

1. 需要训练的数据就是这个用户评分矩阵，这里的训练目标是训练用户的评分
2. 用$Y_{i*}$来表示用户的向量，用$Y_{j*}$来表示item的向量
3. 他们分别过两个不同的MLP层:$$p_i = f_{\theta_N^U}(…f_{\theta_3^U}(W_{U2}f_{\theta_2^U}(Y_{i*W_{U1}}))…) \\ q_i = f_{\theta_N^I}(…f_{\theta_3^I}(W_{I2}f_{\theta_2^I}(Y_{i*W_{I1}}))…)$$
4. 然后对于$p_i$和$p_j$就是用户和item的向量表示，对这两个向量通过cosine求相似度:$$\hat{Y}_{i,j} = F^{DMF}(u_i,v_j|\Theta) = cosine(p_i,q_j) = \frac{p_i^Tq_j}{||p_i|| ||q_j||}$$
5. 最终是使用了一个带权重偏置的交叉熵来优化目标:$$L=-\sum \frac{Y_{i,j}}{\max{R}} \log{\hat{Y}_{_i,j}} + (1-\frac{Y_{i,j}}{\max{R}}) \log(1-{\hat{Y}_{_i,j}}) $$

先来说说这个Loss，里面的$R$为评分的最大值（如果标准的1~5分中$R=5$），因为刚刚说了他其实是要预测分数，分数会有1~5，但同时会有0分，所以这个Loss下当$Y={1~5}$时，他其实是一个将回归问题归一化到0~1的分类问题，当$Y=0$时，他就是一个不折不扣的二分类问题，所以说这个任务下选择这个Loss其实是是挺合适的。

整个模型其实还是很好理解的，看下他的实验结果: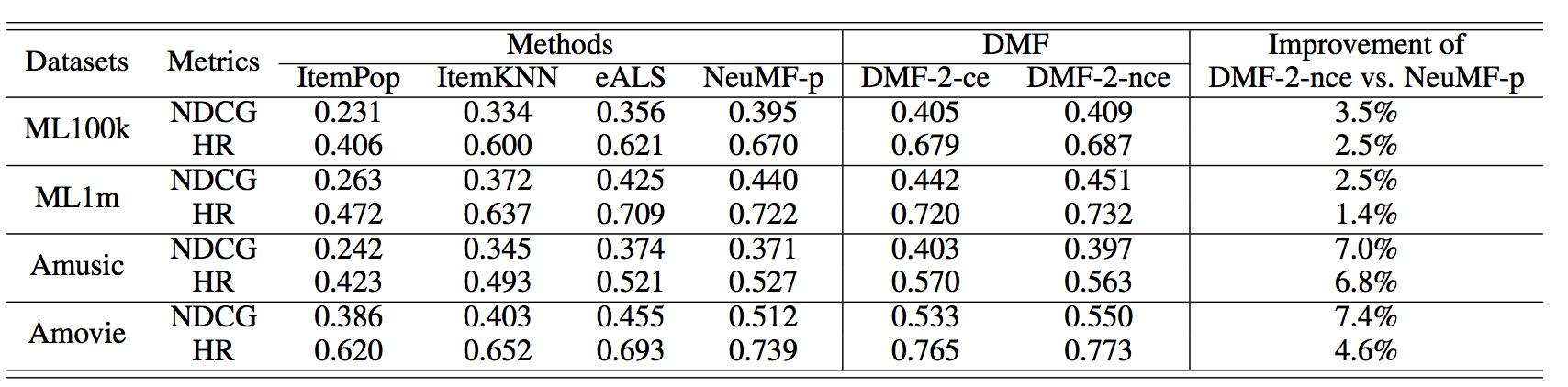

主要对于NeuMF算法，还是有一些些提升的，但是从模型的架构来看，DMF出来除了使用两个单独的MLP，其他与NeuMF的差异并没有很大，模型还是NeuMF更加复杂嘞，个人感觉如果NeuMF使用了pre-train，DMF说不定还无法超过…，同时看了loss改进的提升并不是很多（不过比较符合正常情况-_-）

这里再对比一下DSSM：

1. 一个比较大的区别是DSSM的query和title都是word，都是他的网络是共享的，但是DMF里面其实并不是共享的（我之前的经验，不共享的情况下效果大大折扣。。。)
2. 我觉得DSSM里面最重要的一个点是Pair-Wise的loss学习，但是DMF里面作者也说了，本文用的是PointWise的Loss，对于Pair-Wise的Loss在feature work中使用-_-!!

CMN

传统的矩阵分解和基于DL-embedding的CF方法都是从全局的User-Item矩阵出发，都是只考虑的全局的矩阵。
而CMN（Collaborative Memory Network）的作者针对给定User和Item在算法时，根据Item得到User的最近邻出发，使用最近邻的Embedding来作为局部信息用于CF中，而这里求最近邻的Embedding使用了Memory Network来解。
模型结构还是挺漂亮的：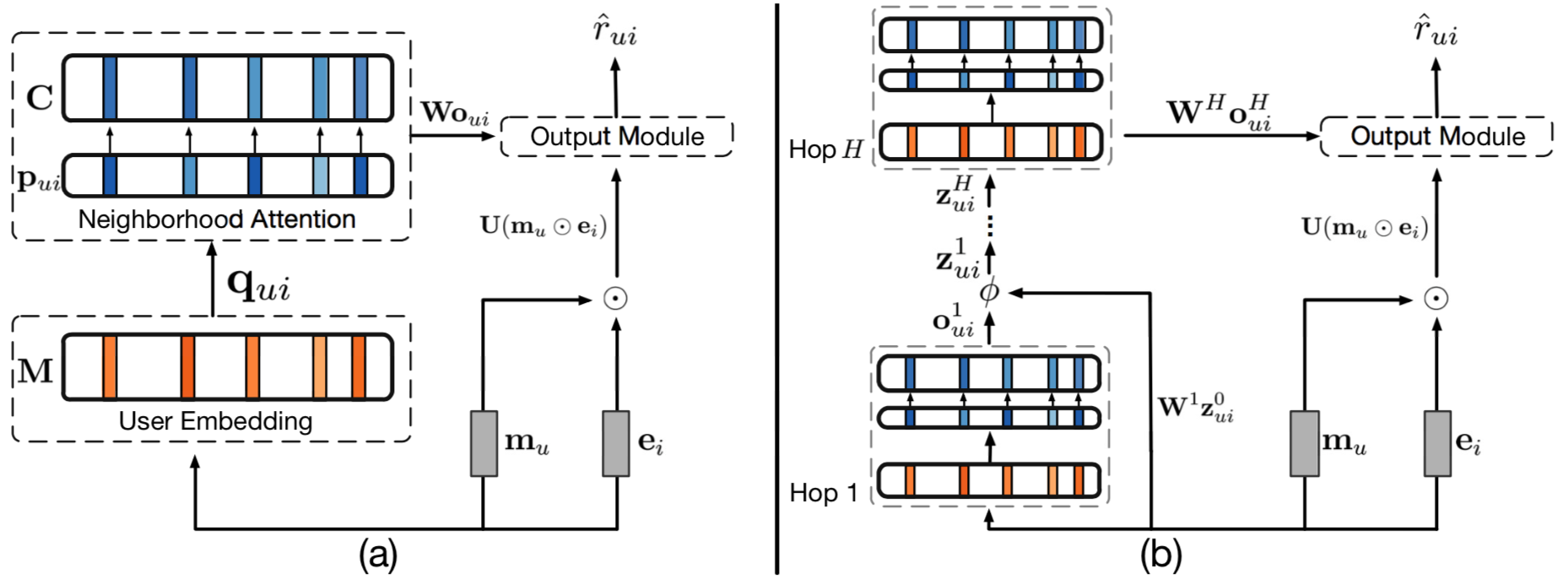

模型主要是分为Glolab信息和Local信息，Glolab和上面两篇文章说的大同小异，上面的结构图主要是通过Memory Network结构来说明Local信息的使用：
整个网络中有三个矩阵:

1. 用户矩阵$M \in R^{P \times d}$，其中$P$为用户量，$m_u$表示单个用户的向量
2. Item矩阵:$E \in R^{Q \times d}$，其中$Q$表示Item数量,$e_i$表示Item的向量
3. 最近邻的Embedding矩阵$C$,大小与$M$一样，用于Memory Network外部矩阵,使用$c_v$来表示单个邻居的向量的

在给定用户$u$和item $i$的情况下，计算$u$和$i$发生交互的用户$v$的距离为：$$q_{uiv} = m_u^T m_v + e_i^T m_v \quad \quad \quad \forall v \in N(i)$$

$N(i)$表示和$i$发生过交互的用户

$q_{uiv}$是内积之后的结果，也就是一个值了，然后使用softmax可以求得各个近邻用户的权重
$$p_{uiv} = \frac{exp(q_{uiv})}{\sum_{k \in N(i)} exp(q_{uik})} \quad \quad \quad \forall v \in N(i)$$

该权重乘以对应的外部矩阵的向量就可以得到当前用户与item最近邻用户的向量了，作为$User$和$Item$的局部信息:
$$o_{ui} = \sum_{v \in N(i)} p_{uiv} c_v$$

最终在输出模型的时候与Glolab信息一起结合进去:
$$\hat{r}_{ui} = v^T \phi (U(m_u \cdot e_i) + W o_{ui} + b)$$

这里CF的距离使用点积的方式，也就是$NumMF$的其中一个子模型版本

刚刚描述的过程就是上图的(a)部分，Memory Network(MN)最大的优势就是可以使用叠加的方式来进行Attention，这样可以使用在后面的MN时会重新调整前面基层的MN，也就是(b)图所示，
这里第一层时$m_u$和$e_i$整合到了一起:$$z^0_{ui} = m_u + e_i$$

邻居用户的算分就可以表示为:$$q_{uiv}^h = (z_{ui}^h)^Tm_v \forall v \in N(i)$$

而其他层的$z$计算为:$$z_{ui}^h = \phi(Wz_{ui}^{h-1} + o_{ui}^h)$$

这种迭代机制正好可以将MN层正好可以堆叠起来，而实验中也是证明了多层的堆叠效果要优于单层的

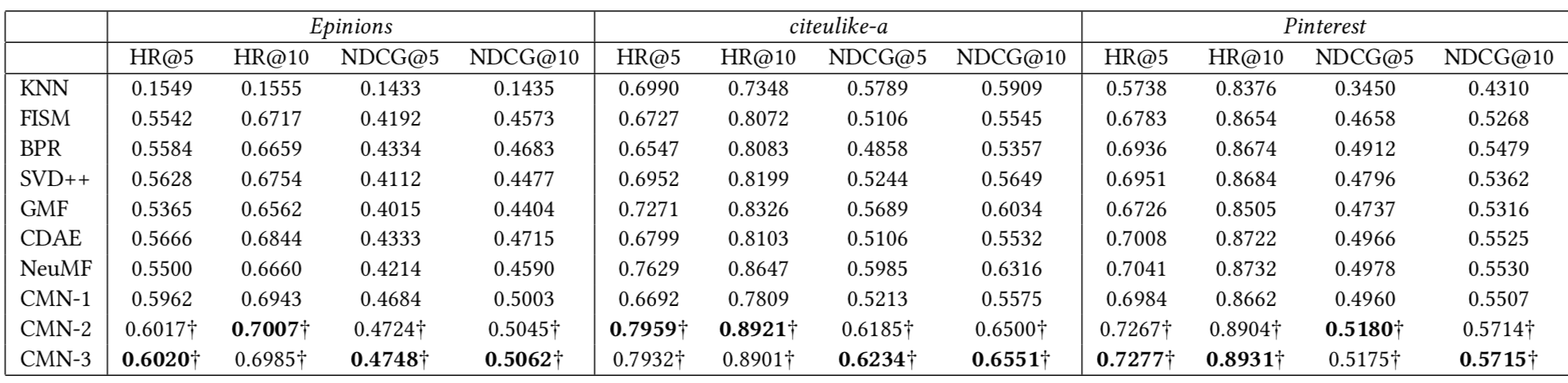
实验结果中主要来对比一下NeuMF，有明显提升同时觉得他的提升比DMF更加合理哈哈，如果在Gbobal这块再做一些细节的处理应该能提升更多。

整个模型的复杂度为:$O(n(d|N(i)| + d^2)+d)$ 而$n$就是MN的层数，因此就模型的工业化而言可行性其实是非常高的，不过需要对$|N(i)|$进行一些剪枝之类的trick处理

DeepCF

这篇paper的作者从CF的Representation和Match两个角度出发：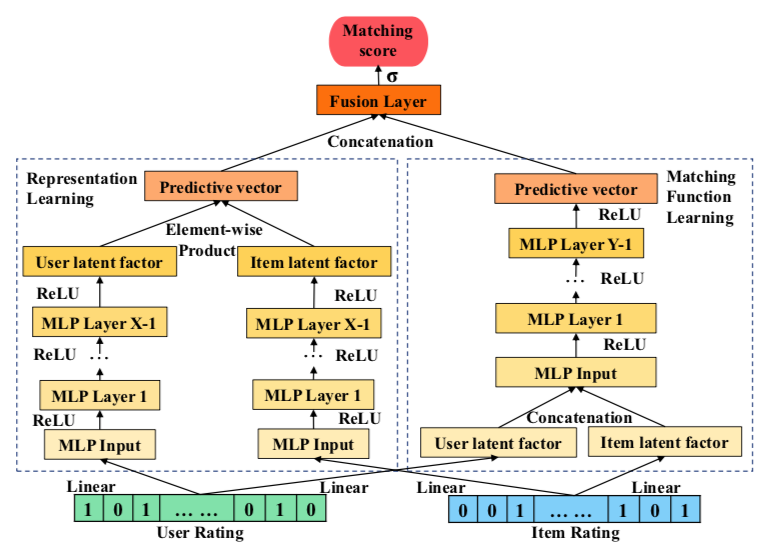

我细看了每天和NeuMF架构没啥差别，除了在GMF那里多了几层MLP -_-，因此细节就不说了。。。

参考

1. Item-Based Collaborative Filtering Recommendation Algorithms
2. BPR: Bayesian Personalized Ranking from Implicit Feedback
3. Deep Matrix Factorization Models for Recommender Systems∗
4. Neural Collaborative Filtering∗
5. Collaborative Memory Network for Recommendation Systems
6. DeepCF -A Unified Framework of Representation Learning and Matching Function Learning in Recommender System